Algebra Relazionale

È un linguaggio “matematico” proposto da E. Codd per poter eseguire operazioni tra tabelle. È basata sulle operazioni sugli insiemi. Essendo un modello matematico gli elementi duplicati non sono ammessi. Ogni riga della tabella viene detta “tupla”.

Il risultato di un’operazione di algebra relazione può essere l’ingresso per un’altra operazione di algebra relazionale! (Composizione di operatori). I principali operatori sono:

Selezione ( σ ). L’operatore esegue una decomposizione orizzontale della tabella, nel senso che estrae solamente alcune tuple (le righe che soddisfano una condizione di selezione). Ma non elimina nessun attributo, infatti lo schema del risultato è identico allo schema della (unica) relazione in ingresso.

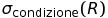
La condizione è una espressione booleana che può contenere operatori di confronto (<,>,<=,>=, =, <>) e connettivi logici (AND, OR)

Proiezione ( π ). La proiezione esegue una decomposizione verticale, nel senso che estrae solamente alcuni attributi. Ma non elimina nessuna tupla (se stiamo parlando di modelli matematiche le tuple identiche vengono collassate in una sola)

Lo schema del risultato contiene solamente i soli attributi contenuti nella lista. L'operatore di proiezione strettamente matematico elimina tuple duplicate, anche se i sistemi reali tipicamente non eliminano i duplicati a meno che l’utente non lo richieda esplicitamente.

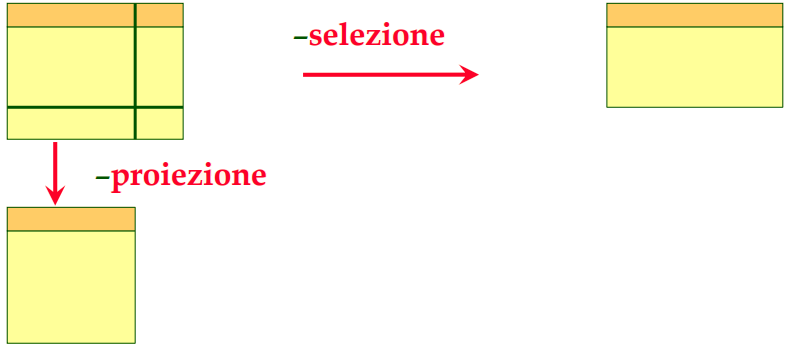
Sono due operatori "ortogonali"

• selezione: decomposizione orizzontale
• proiezione: decomposizione verticale

In quanto “spaccano” la tabella.

Unione ( ∪ ). L'unione di due relazioni R1 e R2 contiene tutte le tuple presenti in R1 o in R2. Le tuple vengono prese una sola volta se esse sono duplicate. Lo schema del risultato è identico allo schema di R1.

R1 ∪ R2

Intersezione ( ∩ ). L'unione di due relazioni R1 e R2 contiene tutte le tuple presenti sia R1 che in R2. Lo schema del risultato è identico allo schema di R1.

R1 ∩ R2

Differenza ( – ). La differenza tra due relazioni R1 e R2 contiene tutte le tuple presenti in R1 ma non in R2. Lo schema del risultato è identico allo schema di R1.

R1 − R2

Ridenominazione ( ρ ). Serve per cambiare nome agli attributi. Si applica ad una relazione R.

Prodotto cartesiano o Cross Join ( × ). Restituisce un’istanza di relazione il cui schema contiene tutti i campi di R1 (nell’ordine originale) seguiti da tutti i campi di R2 (nell’ordine originale).

R1 × R2

(Inner) Join condizionale o theta join ( ⨝ ). Il Join condizionale tra R1 e R2 è una SELECT applicata sul prodotto cartesiano tra R1 e R2.

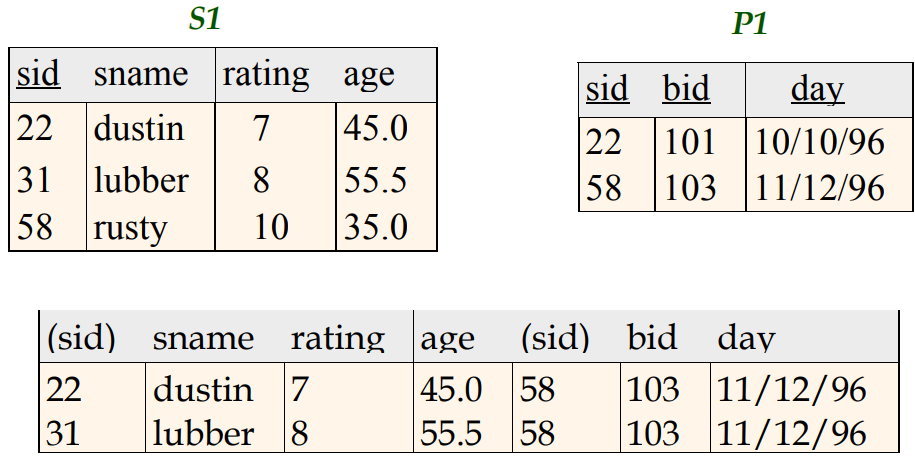
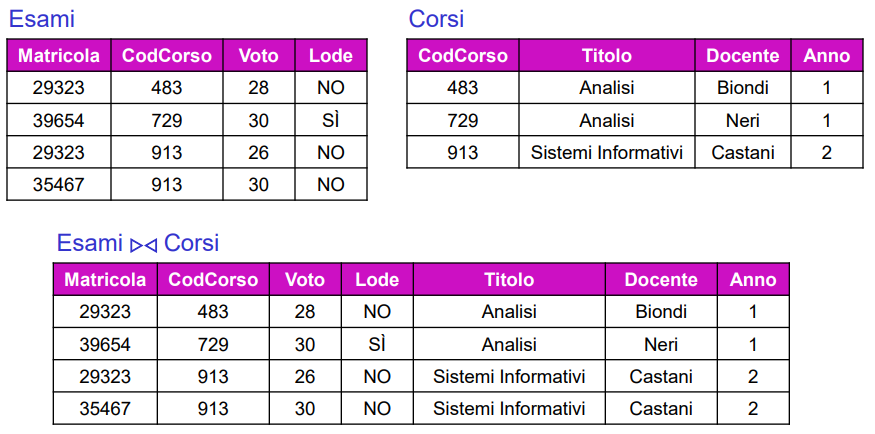
Natural join ( ⨝ ). Equi join su tutti i campi in comune, le uguaglianze sono specificate su tutti gli attributi aventi lo stesso nome in R1 e R2. Senza condizioni.

Le tuple del risultato sono ottenute combinando le tuple degli operandi con valori uguali sugli attributi comuni.

Outer Join. In alcuni casi è utile che anche le tuple dangling di un join compaiano nel risultato. A tale scopo si introduce l’outer join (join “esterno”) che “completa” con valori nulli le tuple dangling. L’outer join include tutte le tuple, assegnando a NULL i campi che non hanno valori corrispondenti. Servono per poter includere le tuple “dangling”, cioè quelle che hanno dei valori NULL negli attributi comuni.

Esistono tre varianti:

• Left ( ⟕, =⨝ o ): solo tuple dell’operando sinistro sono riempite con NULL

• Right ( ⟖, ⨝= o ): idem per l’operando destro

• Full ( ⟗, =⨝= o ): si riempiono con NULL le tuple dangling di entrambi gli operandi

Funzioni aggregate ( F ).